Impressum: Lothar Feige, Schlesierstraße 10 in 78176 Blumberg, Tel. 07702/435772 und e-Mail: webmaster@feinet.de

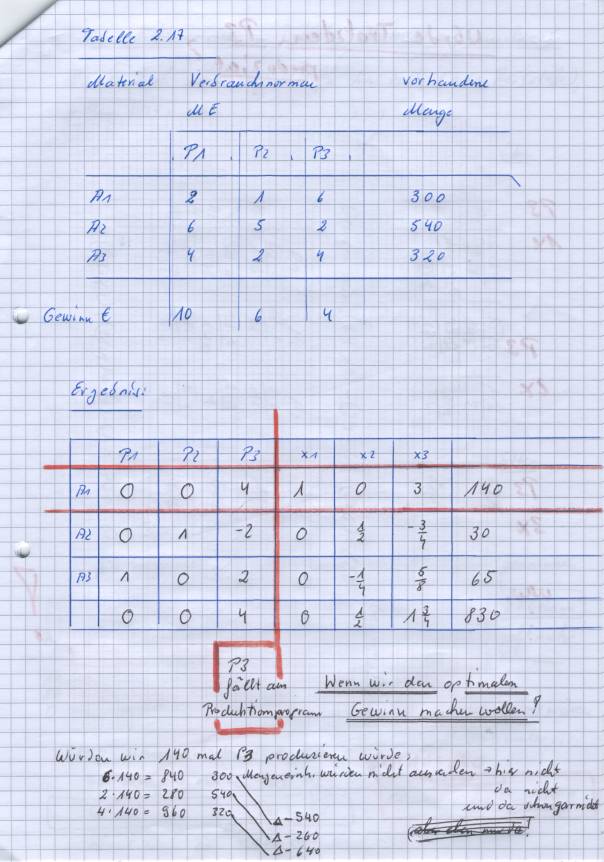
Wir haben folgende Aufgabe:   MAXIMIERUNGSAUFGABE.

Ein Betrieb nutzt die Möglichkeit, kurzfristig aus drei Abfallstoffen, drei Produkte: P1, P2, P3, herzustellen.

Der Reingewinn je Einheit der Produkte lautet:

Für P1 = 10 Euro, für P2 = 6 Euro und für P3 = 4 Euro.

In welcher Anzahl müssen die Produkte hergestellt werden, damit der Reingewinn für dieses Zusatzprogramm möglichst groß wird?

Die Verbrauchsmengen sind folgender Tabelle zu entnehmen:

Tabelle 2.17.                   E steht für Euro!

---------------------------------------------------------------

Material             Verbrauchsmengen,          vorhandene
                     Verbrauchsnormen, ME       Menge (ME)
---------------------------------------------------------------

                     P 1    P 2    P 3

---------------------------------------------------------------

A 1                   2      1      6               340

A 2                   6      5      2               540

A 3                   4      2      4               320

---------------------------------------------------------------

Erlös:               10 E   6 E     4 E            Erlös ist noch
                                                   0 Euro, noch ist
                                                   nix produziert.

Wir bekommen folgende Ungleichungen: 

(P wird zu x (i), A wird zu w (i)) 

2 x1  +  1 x2  +  6 x3  muss sein kleiner oder gleich<  300

6 x1  +  5 x2  +  2 x3  muss sein kleiner oder gleich<  540

4 x1  +  2 x2  +  4 x3  muss sein kleiner oder gleich<  320

----------------------------------------------------------

10 Euro   6 Euro   4 Euro    

unter der Bedingung, das x1 und x2 und x3 mindestens gleich oder größer Null sind.

Jetzt wollen wir langsam zum Simplextableau kommen:

Sprich, aus diesen Ungleichungen machen wir Gleichungen. Wie?

Indem wir zu w1  y1 , zu w2  y2  und zu w3  y3  "zugeben", denn wir wollen ja "Gleichheit erhalten", sprich, linke und rechte Seite der Waage sollen gleich sein!

Aus:

2 x1  +  1 x2  +  6 x3  muss sein kleiner oder gleich<  300

wird:

2 x1  +  1 x2  +  6 x3  + y1                       = 300
----------------------------------------------------------
Aus:

6 x1  +  5 x2  +  2 x3  muss sein kleiner oder gleich<  540

wird:

6 x1  +  5 x2  +  2 x3      +  x y 2                = 540
----------------------------------------------------------
und:

4 x1  +  2 x2  +  4 x3  muss sein kleiner oder gleich<  320
wird:

4 x1  +  2 x2  +  4 x3               + y 3          = 320

----------------------------------------------------------

Der Zielfunktion kommt eine Besonderheit zu, sie wird mit 

- 1 Multipliziert, dadurch wird sie zum Simplexalgorythmus- Simplextablaeu!!! 

10 Euro für w1 und 6 Euro für w2 und 4 Euro für w3 Mal - 1 

= x 1 =>- 10 und x 2 => - 6 und x 3 => - 4 Euro.

Das ganze übertragen wir, in das Simplextableau:

 

	P1 x1	P 2 x2	P3 x3	Y1	Y2	Y3
w1	2	1	6	1	0	0	300
w1	6	5	2	0	1	0	540
w3	4	2	4	0	0	1	320
	-10	-6	-4	0	0	0	Gewinn = 0 E

Wichtig sind alle Elemente, die Zielfunktion wurde mit minus eins multipliziert, jetzt können wir die Aufgabe lösen, mit dem Simplexalgorythmus/Simplextableau:

Gewinnmaximierungsaufgabe, deshalb die Zielfunktion, (um mit dem Simplextableau und Simplexalgorythmus) ausrechnen zu können.

Die Ungleichungen wurden mit Y1 und Y2 und Y3 zu Gleichungen "gemacht".

Zum genauen Ausrechnungsmodus, 

1. Auswahl der Pivotspalte, (anhand des größten Minuswertes in der Zielfunktion),
   

2. Bestimmung der Pivotzeile, die Vorräte werden durch den Wert in der Pivotspalte geteilt,
   300 durch 2 = 150
   540 durch 6 = 90
   320 durch 4 = 80, der kleinste, positive Wert, (GRÖ?ER NULL), ist hier 80, die Pivot-Zeilete ist w3.
   

3. Pivot-element => Zeilenmäßig,  2 mal 1
                                 ---------
                                    2
   

4. Das gleiche nach links und nach rechts, in der  Pivotzeile, auch beim Vorrat,
   

5. Oberhalb und unterhalb der Pivotzeile müssen wir so vorgehen, das wir hier den "Verbrauch" abziehen.

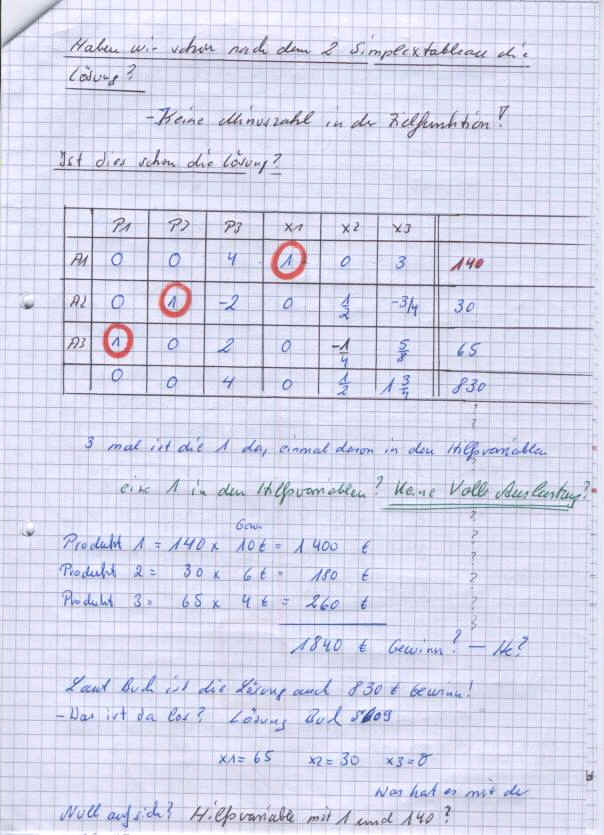
Auch und besonders in der Zielfunktion, - 10 plus 10 mal 1, (auf das Pivotelemt(Ergebnis),  bezogen, nach links und rechts weitergerechnet.

Wem das noch nicht klar ist, ich schlüssel es noch besser auf... 

------------ später ------------ 

Nach dem Zweiten Simplextablau, bzw. dessen Ausrechnung, haben wir in der Zielfunktion keinen Minuswert mehr, wir haben das Optimum erreicht.

(Auch keine 1 ist in der Zielfunktion, sonst hätten wir mehrere Lösungen, bzw. könnten die Lösung noch verbessern. (müssten die Lösung noch verbessern, aber, dazu kommen wir noch, in einer anderen Aufgabe).

Bei der "reinen Gewinnmaximierungsaufgabe" wird wie folgt abgelesen:

Zeile w1   wo ist die Eins?     Rechter Wert aus der letzten "Vorrats-Spalte"

Zeile w2   wo ist die Eins?     Rechter Wert aus der letzten "Vorrats-Spalte"

Zeile w3   wo ist die Eins?     Rechter Wert aus der letzten "Vorrats-Spalte"

Und Ermittlung des "GEWINNS", unten, Zielfunktion auch rechte Spalte.

Keine eins in der Zielfunktion,

Otpimum müsste erreicht sein.

Nochmal kleine Überprüfung:

Der Kaufmann würde nur folgend produzieren: 

1.  was bringt mir den meisten Gewinn,
   

2. was müssen wir dann produzieren, mit dem zweitmeisten Gewinn,
   

3. usw. bis alles soweit aufgebraucht ist, 

das wir die Produktion nicht mehr weiterführen können.

Der Simplexalgorythmus und das Simplextableau verändern auch schon in der ersten Ausrechnung, die Werte in der Zielfunktion!                    DAS führt zum Optimum....

Wenn wir trotzdem Produkt 3 produzieren würden?

Müssen wir dann von einem Anderen Produkt eine ME weniger machen?

Fragen über Fragen.... 

(sehr plakativ)